XIII. On the Graphical Representation of Groups: Groups of Genus Zero and Unity: Cayley’s Colour Groups.

Chapter XIII.
On the Graphical Representation of Groups: Groups of Genus Zero and Unity: Cayley’s Colour Groups.

199. We shall now proceed to a discussion in the cases $p = 0$ and $p = 1$ of the relation

2 (p - 1) = N (n - 2 - \sum_{1}^{n} \frac{1}{m_{r}}),

which connects the number and the orders of the generating operations of a group with the order of the group itself; and to the consideration of the corresponding groups.

For any given value of $p$ , other than $p = 1$ , we may regard this relation as an equation connecting the positive integers $N$ , $n$ , $m_{1}$ , $m_{2}$ , …, $m_{n}$ . It does not however follow from the investigations of the last Chapter that there is always a group or a set of groups corresponding to a given solution of the equation. In fact, for values of $p$ greater than $1$ , this is not necessarily the case. We shall however ﬁnd that, when $p = 0$ , there is a single type of group corresponding to each solution of the equation; and that, when $p = 1$ , there is an inﬁnite number of types of group, all characterized by a common property, corresponding to each solution of the equation. When $p = 0$ , the groups are (§ 196) of genus zero; and all possible groups of genus zero are found by putting $p = 0$ in the equation. The groups thus obtained are of special importance in many applications of group-theory; for this reason, they will be dealt with in considerable detail.

200. When $p = 0$ , the equation may be written in the form

2 (1 - \frac{1}{N}) = \sum_{1}^{n} (1 - \frac{1}{m_{r}});

in this form, it is clear that the only admissible values of

n

are

2

and

3

First, let $n = 2$ . The only possible solution then is

N = m_{1} = m_{2} = n,

n

being any integer. The corresponding group is a cyclical group of order

n

Secondly, let $n = 3$ . In this case, one at least of the three integers $m_{1}$ , $m_{2}$ , $m_{3}$ must be equal to $2$ , as otherwise the right-hand side of the equation would be not less than $2$ . We may therefore without loss of generality put $m_{1} = 2$ . If now both $m_{2}$ and $m_{3}$ were greater than $3$ , the right-hand side would still be not less than $2$ ; and therefore we may take $m_{2}$ to be either $2$ or $3$ . When $m_{1}$ and $m_{2}$ are both $2$ , the equation becomes

\frac{2}{N} = \frac{1}{m_{3}};

giving

m_{3} = n, N = 2 n,

where

n

is any integer.

When $m_{1}$ is $2$ and $m_{2}$ is $3$ , the equation is

\frac{2}{N} + \frac{1}{6} = \frac{1}{m_{3}} .

This has three solutions in positive integers; namely,

\begin{array}{l} m_{3} & = 3, & N & = 12; \\ m_{3} & = 4, & N & = 24; \\ a n d m_{3} & = 5, & N & = 60 . \end{array}

The solutions of the equation for the case $p = 0$ may therefore be tabulated in the form:—

	$m_{1}$	$m_{2}$	$m_{3}$	$N$


I	n	n		n


II	2	2	n	2n


III	2	3	3	12


IV	2	3	4	24


V	2	3	5	60

201. That a single type of group actually exists, corresponding to each of these solutions, may be seen at once by returning to our plane ﬁgure. The sum of the internal angles of the triangle $A_{1} A_{2} A_{3}$ formed by circular arcs is, in each of these cases, greater than two right angles; and the common orthogonal circle is therefore imaginary. The complete ﬁgure will therefore divide the whole plane into black and white triangles, so that there are no boundaries to consider. Moreover, the number of white triangles in each case must be equal to the corresponding value of $N$ ; for the preceding investigation shews that this is a possible value, and on the other hand the process, by which the ﬁgure is completed from a given original triangle, is a unique one. There is therefore a group corresponding to each solution; and the correspondence which has been established in any case between the operations of a group and the polygons of a ﬁgure, proves that there cannot be two distinct types of group corresponding to the same solution.

202. The plane ﬁgure for $p = 0$ does not, in fact, diﬀer essentially from the ﬁgure drawn on a continuous simply connected surface in space. The former may be regarded as the stereographic projection of the latter. The ﬁve distinct types are represented graphically by the following ﬁgures.

The ﬁrst is a cyclical group, and the ﬁgure (ﬁg. 9) does not diﬀer essentially from ﬁg. 2 in § 183.

The group given by the second solution of the equation is called the dihedral group. It is represented by ﬁg. 10.

pict

The group given by the third solution of the equation is represented in ﬁg. 11. It is known as the tetrahedral group.

To the fourth solution of the equation corresponds the group represented by ﬁg. 12. It is known as the octohedral group.

To the ﬁfth solution of the equation corresponds the group represented in ﬁg. 13. It is known as the icosahedral group.

The four last groups are identical with the groups of rotations which will bring respectively a double pyramid on an $n$ -sided base, a tetrahedron, an octohedron, and an icosahedron to coincidence with itself in each case⁸⁰.

When the ﬁgures are drawn on a sphere, and the three circles of the original triangle and therefore also all the circles of the ﬁgure are taken to be great-circles of the sphere, the actual displacements of the triangles among themselves which correspond

pict

to the operations of the group can be eﬀected by real rotations about diameters of the sphere; thus the statement of the preceding sentence may be directly veriﬁed.

203. In terms of their generating operations, the ﬁve types of group of genus zero are given by the relations:—

\begin{array}{l} I. & S_{1}^{n} & = 1, & S_{2}^{n} & = 1, & S_{1} S_{2} & = 1; \\ II. & S_{1}^{2} & = 1, & S_{2}^{2} & = 1, & S_{3}^{n} & = 1, & S_{1} S_{2} S_{3} & = 1; \\ III. & S_{1}^{2} & = 1, & S_{2}^{3} & = 1, & S_{3}^{3} & = 1, & S_{1} S_{2} S_{3} & = 1; \\ IV. & S_{1}^{2} & = 1, & S_{2}^{3} & = 1, & S_{3}^{4} & = 1, & S_{1} S_{2} S_{3} & = 1; \\ V. & S_{1}^{2} & = 1, & S_{2}^{3} & = 1, & S_{3}^{5} & = 1, & S_{1} S_{2} S_{3} & = 1 . \end{array}

The ﬁrst of these does not require special discussion.

In the dihedral group, we have

S_{1} S_{3} S_{1} = S_{1} S_{2} = S_{3}^{- 1} .

The dihedral group of order $2 n$ therefore contains a cyclical sub-group of order $n$ self-conjugately; and every operation of the group which does not belong to this self-conjugate sub-group is of order $2$ . The operations of the group are given, each once and once only, by the form

S_{1}^{α} S_{3}^{β}, (α = 0, 1; β = 0, 1, 2, \dots, n - 1) .

When $n = 3$ , this group is simply isomorphic with the symmetric group of three symbols.

In the tetrahedral group, since

\begin{matrix} {(S_{1} S_{2})}^{3} = 1, \\ S_{2}^{- 1} S_{1} S_{2} S_{1} = S_{2} S_{1} S_{2}^{- 1}, \end{matrix}

and therefore $S_{1}$ , $S_{2}^{- 1} S_{1} S_{2}$ , $S_{2} S_{1} S_{2}^{- 1}$ are permutable with each other. These operations of order $2$ (with identity) form a self-conjugate sub-group of order $4$ ; and the $12$ operations of the group are therefore given by the form

S_{2}^{α} {(S_{2}^{- 1} S_{1} S_{2})}^{β} S_{1}^{γ},

S_{2}^{α} S_{1}^{β} S_{2} S_{1}^{γ}, (α = 0, 1, 2; β, γ = 0, 1) .

S_{1} = (12) (34), S_{2} = (123),

then

S_{1} S_{2} = (134);

and therefore the tetrahedral group is simply isomorphic with the alternating group of four symbols.

If, in the octohedral group, we write

S_{3}^{2} = S',

then

S_{2} S' = S_{1} S_{3} = S_{1} S_{2}^{2} S_{1};

and therefore

{(S_{2} S')}^{3} = 1 .

Hence $S_{2}$ and $S'$ generate a tetrahedral group.

Again

S_{1} S_{2} S_{1} = {(S_{2} S')}^{2},

and

S_{1} S' S_{1} = S_{2} S' S_{2}^{- 1},

so that this is a self-conjugate sub-group. The operations of the group are given, each once and once only, in the form

S_{1}^{α} S_{2}^{β} S_{3}^{2 γ} S_{2} S_{3}^{2 δ}, (α, γ, δ = 0, 1; β = 0, 1, 2) .

S_{1} = (12), S_{2} = (234),

then

S_{1} S_{2} = (1342);

and therefore the octohedral group is simply isomorphic with the symmetric group of four symbols.

The icosahedral group is simple. It is, in fact, simply isomorphic with the alternating group of ﬁve symbols which has been shewn (§ 111) to be a simple group. Thus if

S_{1} = (12) (34), S_{2} = (135),

then

S_{1} S_{2} = (12345);

so that the substitutions

S_{1}

and

S_{2}

satisfy the relations

S_{1}^{2} = 1, S_{2}^{3} = 1, {(S_{1} S_{2})}^{5} = 1 .

They must therefore generate an icosahedral group or one of its sub-groups. On the other hand, from the substitutions $S_{1}$ and $S_{2}$ all the even substitutions of ﬁve symbols may be formed, and these are $60$ in number. The group therefore cannot be a sub-group of the icosahedral group; the only alternative is that the two are identical.

As the icosahedral group has no self-conjugate group, we cannot in this case so easily construct a form which will represent each operation of the group just once in terms of the generating operations. It is however not diﬃcult to verify that this is true of the set of forms⁸¹

\begin{gathered} S_{3}^{α}, S_{3}^{α} S_{1} S_{3}^{β}, S_{3}^{α} S_{1} S_{3}^{2} S_{1} S_{3}^{β}, \\ S_{3}^{α} S_{1} S_{3}^{2} S_{1} S_{3}^{3} S_{1}, \end{gathered} (α, β = 0, 1, 2, 3, 4) .

204. We shall next deal with the equation in the case $p = 1$ . In this case alone, the order of the group disappears from the equation, which merely gives a relation between the number and order of the generating operations. This may be written in the form

2 = \sum_{1}^{n} (1 - \frac{1}{m_{r}});

and

n

must therefore be either

4

3

When $n$ is $4$ , the equation becomes

2 = \frac{1}{m_{1}} + \frac{1}{m_{2}} + \frac{1}{m_{3}} + \frac{1}{m_{4}},

and the only solution is clearly

m_{1} = m_{2} = m_{3} = m_{4} = 2 .

When $n$ is $3$ , the equation takes the form

1 = \frac{1}{m_{1}} + \frac{1}{m_{2}} + \frac{1}{m_{3}},

and is easily seen to have three solutions, viz.

\begin{array}{l} m_{1} & = 3, & m_{2} & = 3, & m_{3} & = 3; \\ m_{1} & = 2, & m_{2} & = 4, & m_{3} & = 4; \\ a n d m_{1} & = 2, & m_{2} & = 3, & m_{3} & = 6 . \end{array}

205. Take ﬁrst the solution

n = 4, m_{1} = m_{2} = m_{3} = m_{4} = 1 .

The corresponding general group is deﬁned by the relations

\begin{matrix} S_{1}^{2} = 1, S_{2}^{2} = 1, S_{3}^{2} = 1, S_{4}^{2} = 1, \\ S_{1} S_{2} S_{3} S_{4} = 1 . \end{matrix}

If we proceed to form the plane ﬁgure representing this group, the sum of the internal angles of the quadrilateral $A_{1} A_{2} A_{3} A_{4}$ is equal to four right angles, and the four circles that form it therefore pass through a point. If this point be taken at inﬁnity, the four circles (and therefore all the circles of the ﬁgure) become straight lines. The plane ﬁgure will now take the form given in ﬁg. 14, and the four generating operations are actual rotations through two right angles about lines through $A_{1}$ , $A_{2}$ , $A_{3}$ and $A_{4}$ , perpendicular to the plane of the ﬁgure.

pict

Every operation of the group is therefore, in this form of representation, either a rotation through two right angles about a corner of the ﬁgure or a translation; and it will clearly be the former or the latter according as it consists of an odd or an even number of factors, when expressed in terms of the generating operations. The operations which correspond to translations form a sub-group; for if two operations each consist of an even number of factors, so also does their product. Moreover, this sub-group is self-conjugate, since the number of factors in $Σ^{- 1} S Σ$ is even if the number in $S$ is even. This self-conjugate sub-group is generated by the two operations

S_{1} S_{2} and S_{2} S_{3};

for

\begin{matrix} S_{1} S_{3} = S_{1} S_{2} \cdot S_{2} S_{3}, \\ S_{2} S_{1} = {(S_{1} S_{2})}^{- 1}, S_{3} S_{2} = {(S_{2} S_{3})}^{- 1}, S_{3} S_{1} = {(S_{2} S_{3})}^{- 1} {(S_{1} S_{2})}^{- 1}; \end{matrix}

and therefore every operation containing an even number of factors can be represented in terms of $S_{1} S_{2}$ and $S_{2} S_{3}$ . Lastly, these two operations are permutable with each other; for

S_{2} S_{3} \cdot S_{1} S_{2} = S_{2} S_{3} \cdot S_{4} S_{3} = S_{1} S_{3} = S_{1} S_{2} \cdot S_{2} S_{3};

and therefore every operation of the group is contained, once and only once, in the form

S_{1}^{α} {(S_{1} S_{2})}^{β} {(S_{2} S_{3})}^{γ}, (α = 0, 1 : β, γ = - \infty, \dots, 0, \dots, \infty) .

The results thus arrived at may also be veriﬁed very simply by purely kinematical considerations. If a group generated by $S_{1}$ , $S_{2}$ , $S_{3}$ and $S_{4}$ is of ﬁnite order, there must, since it is of genus $1$ , be either one or two additional relations between the generating operations; and any such relation is expressible by equating the symbol of some operation of the general group to unity. Such a relation is therefore either of the form

S_{1} {(S_{1} S_{2})}^{b} {(S_{2} S_{3})}^{c} = 1,

{(S_{1} S_{2})}^{b} {(S_{2} S_{3})}^{c} = 1 .

The operation $S_{1} {(S_{1} S_{2})}^{b} {(S_{2} S_{3})}^{c}$ of the general group, consisting of an odd number of factors, must be a rotation round some corner of the ﬁgure, say a rotation round the corner $A_{r}$ of the white quadrilateral $Σ$ ; it is therefore identical with $Σ^{- 1} S_{r} Σ$ .

Now the relation

Σ^{- 1} S_{r} Σ = 1,

gives

S_{r} = 1 .

A relation of the ﬁrst of the two forms is therefore inconsistent with the supposition that the group is actually generated by $S_{1}$ , $S_{2}$ and $S_{3}$ . It, in fact, reduces the generating operations and the relations among them to

S_{1}^{2} = 1, S_{2}^{2} = 1, S_{3}^{2} = 1, S_{1} S_{2} S_{3} = 1,

which deﬁne a group of genus zero.

The only admissible relations for a group of genus $1$ are therefore those of the form

{(S_{1} S_{2})}^{b} {(S_{2} S_{3})}^{c} = 1 .

A single relation of this form reduces the operations of the general group to those contained in

\begin{matrix} S_{1}^{α} {(S_{1} S_{2})}^{β} {(S_{2} S_{3})}^{γ}, \\ (α = 0, 1; β = 0, 1, \dots, b - 1; γ = - \infty, \dots, 0, \dots, \infty); \end{matrix}

and the group so deﬁned is still of inﬁnite order.

Finally, two independent relations

\begin{matrix} {(S_{1} S_{2})}^{b} {(S_{2} S_{3})}^{c} = 1, \\ {(S_{1} S_{2})}^{b'} {(S_{2} S_{3})}^{c'} = 1, \end{matrix}

where

\frac{b}{b'} \neq \frac{c}{c'},

must necessarily lead to a group of ﬁnite order. If

m

is the greatest common factor of

b

and

b'

, so that

b = b_{1} m, b' = b' m,

where

b_{1}

and

b'

are relatively prime; and if

b_{1} x - b' y = 1;

the two relations give

{(S_{2} S_{3})}^{c b' - c' b_{1}} = 1,

and

{(S_{1} S_{2})}^{m} = {(S_{2} S_{3})}^{c' y - c x} .

Every operation of the group is now contained, once and only once, in the form

\begin{matrix} S_{1}^{α} {(S_{1} S_{2})}^{β} {(S_{2} S_{3})}^{γ}, \\ (α = 0, 1; β = 0, 1, \dots, m - 1; γ = 0, 1, \dots, c b' - b_{1} c' - 1); \end{matrix}

and the order of the group is $2 (b c' - b' c)$ .

206. Corresponding to the solution

n = 3, m_{1} = m_{2} = m_{3} = 3,

we have the general group generated by

S_{1}

S_{2}

S_{3}

, where

\begin{matrix} S_{1}^{3} = 1, S_{2}^{3} = 1, S_{3}^{3} = 1, \\ S_{1} S_{2} S_{3} = 1 . \end{matrix}

The sum of the three angles of the triangle $A_{1} A_{2} A_{3}$ is two

pict

right angles, and therefore again the circles in the plane ﬁgure (ﬁg. 15) may be taken as straight lines. When the ﬁgure is thus chosen, the generating operations are rotations through $\frac{2}{3} π$ about the angles of an equilateral triangle; and every operation of the group is either a translation or a rotation.

The three operations

S_{1} S_{2}^{2}, S_{2} S_{1} S_{2}, S_{2}^{2} S_{1},

when transformed by

S_{2}

, are interchanged among themselves. When transformed by

S_{1}

they become

S_{2}^{2} S_{1}, S_{1}^{2} S_{2} S_{1} S_{2} S_{1}, S_{1}^{2} S_{2}^{2} S_{1}^{2},

and since

{(S_{1} S_{2})}^{3} = 1,

the two latter are

S_{1} S_{2}^{2}

and

S_{2} S_{1} S_{2}

respectively.

Hence the three operations generate a self-conjugate sub-group; and since

S_{1} S_{2}^{2} \cdot S_{2} S_{1} S_{2} \cdot S_{2}^{2} S_{1} = 1,

this sub-group is generated by

S_{1} S_{2}^{2}

and

S_{2} S_{1} S_{2}

These two operations are permutable; for

S_{1} S_{2}^{2} \cdot S_{2} S_{1} S_{2} = S_{1}^{2} S_{2} = S_{2} S_{1} S_{2} S_{1} S_{2} \cdot S_{2} = S_{2} S_{1} S_{2} \cdot S_{1} S_{2}^{2} .

Hence ﬁnally, every operation of the group is represented, once and only once, by the form

S_{1}^{α} {(S_{1} S_{2}^{2})}^{β} {(S_{2} S_{1} S_{2})}^{γ}, (α = 0, 1, 2; β, γ = - \infty, \dots, 0, \dots, \infty) .

This result might also be arrived at by purely kinematical considerations; for an inspection of the ﬁgure shews that the two simplest translations are

S_{1} S_{2}^{2} and S_{2} S_{1} S_{2},

and that every translation in the group can be obtained by the combination and repetition of these. Every operation in which the index

α

is not zero must be a rotation through

\frac{2}{3} π

\frac{4}{3} π

about one of the angles of the ﬁgure; it is therefore necessarily identical with an operation of the form

Σ^{- 1} S_{r}^{α} Σ .

If now the group generated by $S_{1}$ , $S_{2}$ , $S_{3}$ is of ﬁnite order, there must be either one or two additional relations between them. A relation of the form

S_{1}^{a} {(S_{1} S_{2}^{2})}^{b} {(S_{2} S_{1} S_{2})}^{c} = 1,

where

a

is either

1

2

, is equivalent to

Σ^{- 1} S_{r}^{a} Σ = 1,

so that

S_{r} = 1 .

Such a relation would reduce the group to a cyclical group of order

3

. This is not admissible, if the group is actually to be generated by two distinct operations

S_{1}

and

S_{2}

A relation

{(S_{1} S_{2}^{2})}^{b} {(S_{2} S_{1} S_{2})}^{c} = 1,

gives, on transformation by

S_{2}^{- 1}

{(S_{2} S_{1} S_{2})}^{b} {(S_{2}^{2} S_{1})}^{c} = 1 .

Now

S_{2}^{2} S_{1} = {(S_{1} S_{2}^{2})}^{- 1} {(S_{2} S_{1} S_{2})}^{- 1},

so that

{(S_{1} S_{2}^{2})}^{- c} {(S_{2} S_{1} S_{2})}^{b - c} = 1 .

If $m$ is the greatest common factor of $b$ and $c$ , so that

b = b' m, c = c' m,

where

b'

and

c'

are relatively prime; and if

b' x - c' y = 1,

the two relations

{(S_{1} S_{2}^{2})}^{b} {(S_{2} S_{1} S_{2})}^{c} = 1,

and

{(S_{1} S_{2}^{2})}^{- c} {(S_{2} S_{1} S_{2})}^{b - c} = 1,

lead to

{(S_{2} S_{1} S_{2})}^{m ({b'}^{2} - b' c' + {c'}^{2})} = 1,

and

{(S_{1} S_{2})}^{m} = {(S_{2} S_{1} S_{2})}^{m {(c' - b') y - c' x}};

and every operation of the group is contained, once and only once, in the form

S_{1}^{α} {(S_{1} S_{2}^{2})}^{β} {(S_{2} S_{1} S_{2})}^{γ},

where

α = 0, 1, 2; β = 0, 1, \dots, m - 1; γ = 0, 1, \dots, m ({b'}^{2} - b' c' + {c'}^{2}) - 1 .

Thus the group is of ﬁnite order

3 (b^{2} - b c + c^{2})

. In this case then, unlike the previous one, a single additional relation is suﬃcient to ensure that the group is of ﬁnite order. Any further relation, which is independent, must of necessity reduce the group to a cyclical group of order

3

or to the identical operation.

207. The two remaining solutions may now be treated in less detail. The general group corresponding to the solution

n = 3, m_{1} = 2, m_{2} = m_{3} = 4,

is given by

\begin{matrix} S_{1}^{2} = 1, S_{2}^{4} = 1, S_{3}^{4} = 1, \\ S_{1} S_{2} S_{3} = 1, \end{matrix}

and is represented graphically by ﬁg. 16.

pict

All the translations of the group can be generated from the two operations

S_{1} S_{2}^{2}, S_{2} S_{1} S_{2};

and every operation of the group is given, once and only once, by the form

S_{2}^{α} {(S_{1} S_{2}^{2})}^{β} {(S_{2} S_{1} S_{2})}^{γ}, (α = 0, 1, 2, 3; β, γ = - \infty, \dots, 0, \dots, \infty) .

An additional relation of the form

S_{2}^{a} {(S_{1} S_{2}^{2})}^{b} {(S_{2} S_{1} S_{2})}^{c} = 1,

where

a

1

2

3

, leads either to

S_{1} = 1, S_{2} = 1 or S_{3} = 1,

and is therefore inconsistent with the supposition that the group is generated by two distinct operations.

An additional relation

{(S_{1} S_{2}^{2})}^{b} {(S_{2} S_{1} S_{2})}^{c} = 1

gives

{(S_{1} S_{2}^{2})}^{- c} {(S_{2} S_{1} S_{2})}^{b} = 1 :

and if

\begin{matrix} b = b_{1} m, c = c_{1} m, \\ b_{1} x + c_{1} y = 1, \end{matrix}

where $b_{1}$ and $c_{1}$ are relatively prime, these relations are equivalent to

\begin{matrix} {(S_{2} S_{1} S_{2})}^{m (b_{1}^{2} + c_{1}^{2})} = 1, \\ {(S_{1} S_{2}^{2})}^{m} = {(S_{2} S_{1} S_{2})}^{m (b_{1} y - c_{1} x)} . \end{matrix}

Every operation of the group is then contained, once and only once, in the form

\begin{matrix} S_{2}^{α} {(S_{1} S_{2}^{2})}^{β} {(S_{2} S_{1} S_{2})}^{γ}, \\ (α = 0, 1, 2, 3; β = 0, 1, \dots, m - 1; γ = 0, 1, \dots, m (b_{1}^{2} + c_{1}^{2}) - 1); \end{matrix}

and the order of the group is $4 (b^{2} + c^{2})$ .

208. Lastly, the general group corresponding to the solution

n = 3, m_{1} = 2, m_{2} = 3, m_{3} = 6,

is given by

\begin{matrix} S_{1}^{2} = 1, S_{2}^{3} = 1, S_{3}^{6} = 1, \\ S_{1} S_{2} S_{3} = 1; \end{matrix}

and it is represented graphically by ﬁg. 17.

pict

Now it may again be veriﬁed, either from the generating relations or from the ﬁgure, that the two operations

S_{2}^{2} S_{3}^{2} and S_{3} S_{2}^{2} S_{3},

which are permutable with each other, generate all the operations which in the kinematical form of the group are translations; and that every operation of the group is represented, once and only once, by the form

\begin{matrix} S_{3}^{α} {(S_{2}^{2} S_{3}^{2})}^{β} {(S_{3} S_{2}^{2} S_{3})}^{γ}, \\ (α = 0, 1, \dots, 5; β, γ = - \infty, \dots, 0, \dots, \infty) . \end{matrix}

Also as before, any further relation, which does not reduce the group to a cyclical group, is necessarily of the form

{(S_{2}^{2} S_{3}^{2})}^{b} {(S_{3} S_{2}^{2} S_{3})}^{c} = 1 .

On transforming this relation by $S_{3}^{- 1}$ we obtain

{(S_{3} S_{2}^{2} S_{3})}^{b} {(S_{3}^{2} S_{2}^{2})}^{c} = 1 .

Now

S_{3}^{2} S_{2}^{2} = {(S_{2}^{2} S_{3}^{2})}^{- 1} (S_{3} S_{2}^{2} S_{3});

so that

{(S_{2}^{2} S_{3}^{2})}^{- c} {(S_{3} S_{2} S_{3})}^{b + c} = 1 .

If then

\begin{matrix} b = b_{1} m, c = c_{1} m, \\ b_{1} x + c_{1} y = 1, \end{matrix}

where $b_{1}$ and $c_{1}$ are relatively prime, it follows that

{(S_{3} S_{2}^{2} S_{3})}^{m (b_{1}^{2} + b_{1} c_{1} + c_{1}^{2})} = 1,

and

{(S_{2}^{2} S_{3}^{2})}^{m} = {(S_{3} S_{2} S_{3})}^{m {b_{1} y + c_{1} (y - x)}} .

Every operation of the group is then contained, once and only once, in the form

\begin{matrix} S_{3}^{α} {(S_{2}^{2} S_{3}^{2})}^{β} {(S_{3} S_{2}^{2} S_{3})}^{γ}, \\ (α = 0, 1, \dots, 5; β = 0, 1, \dots, m - 1; γ = 0, 1, \dots, m (b_{1}^{2} + b_{1} c_{1} + c_{1}^{2}) - 1); \end{matrix}

and the order of the group is $6 (b^{2} + b c + c^{2})$ .

209. There are thus four distinct classes of groups⁸² of genus $1$ , which are deﬁned in terms of their generating operations by the following sets of relations:—

I. $\begin{gathered} S_{1}^{2} = 1, S_{2}^{2} = 1, S_{3}^{2} = 1, {(S_{1} S_{2} S_{3})}^{2} = 1, \\ {(S_{1} S_{2})}^{a} {(S_{2} S_{3})}^{b} = 1, {(S_{1} S_{2})}^{a'} {(S_{2} S_{3})}^{b'} = 1, (a b' - a' b > 0); \\ N = 2 (a b' - a' b) . \end{gathered}$

II. $\begin{gathered} S_{1}^{3} = 1, S_{2}^{3} = 1, {(S_{1} S_{2})}^{3} = 1, \\ {(S_{1}^{2} S_{2}^{2})}^{a} {(S_{2} S_{1} S_{2})}^{b} = 1; \\ N = 3 (a^{2} - a b + b^{2}) . \end{gathered}$

III. $\begin{gathered} S_{1}^{2} = 1, S_{2}^{4} = 1, {(S_{1} S_{2})}^{4} = 1, \\ {(S_{1} S_{2}^{2})}^{a} {(S_{2} S_{1} S_{2})}^{b} = 1; \\ N = 4 (a^{2} + b^{2}) . \end{gathered}$

IV. $\begin{gathered} S_{1}^{6} = 1, S_{2}^{3} = 1, {(S_{1} S_{2})}^{2} = 1, \\ {(S_{1}^{2} S_{2}^{2})}^{a} {(S_{1} S_{2}^{2} S_{1})}^{b} = 1; \\ N = 6 (a^{2} + a b + b^{2}) . \end{gathered}$

For special values of $a$ and $b$ , some of these groups may be groups of genus zero; for instance, in Class I, if $a b' - a' b$ is a prime, the group is a dihedral group. It is left as an exercise to the reader to determine all such exceptional cases.

Ex. Prove that the number of distinct types of group, of genus two, is three; viz. the groups deﬁned by

\begin{array}{l} (i) & A^{4} & = 1, & B^{2} & = A^{2}, & B^{- 1} A B = A^{- 1}; \\ (ii) & A^{8} & = 1, & B^{2} & = 1, & B^{- 1} A B = A^{3}; \\ (iii) & A^{8} & = 1, & B^{2} & = 1, & {(A B)}^{3} = 1, {(A^{4} B)}^{2} = 1 . \end{array}

210. As a ﬁnal illustration of the present method of graphical representation, we will consider the simple group of order $168$ (§ 146), given by

{(1236457), (234) (567), (2763) (45)} .

The operations of this group are of orders $7$ , $4$ , $3$ and $2$ ; and it is easy to verify that three operations of orders $2$ , $3$ , and $7$ can be chosen such that their product is identity.

In fact, if

S_{2} = (16) (34), S_{3} = (253) (476), S_{7} = (1673524);

then

S_{2} S_{3} S_{7} = 1 .

Moreover, these three operations generate the group. The connectivity of the corresponding surface, by the regular division of which the group can be represented, is $2 p + 1$ ; where

2 p - 2 = 168 (3 - 2 - \frac{1}{2} - \frac{1}{3} - \frac{1}{7}) .

This gives

p = 3;

it follows from Theorem II, § 197, that the genus of the group is

3

The ﬁgure for the general group, generated by $S_{2}$ , $S_{3}$ , and $S_{7}$ , where

\begin{matrix} S_{2}^{2} = 1, S_{3}^{3} = 1, S_{7}^{7} = 1, \\ S_{2} S_{3} S_{7} = 1, \end{matrix}

acquires as symmetrical a form as possible, by taking the centre of the orthogonal circle for that angular point of the triangle $1$ at which the angle is $\frac{1}{7} π$ . In ﬁg. 18 a portion of the general ﬁgure, which is contained between two radii of the orthogonal circle inclined at an angle $\frac{2}{7} π$ , is shewn. The remainder may be ﬁlled in by inversions at the diﬀerent portions of the boundary.

pict

The operations, which correspond to the white triangles of the ﬁgure, are given by the following table:—

\begin{matrix} 1 & 1 & 9 & S_{2} S_{7}^{5} S_{2} & 17 & S_{2} S_{7}^{5} S_{2} S_{7}^{3} S_{2} \\ 2 & S_{2} & 10 & S_{7} S_{2} S_{7}^{5} S_{2} & 18 & S_{7}^{6} S_{2} S_{7}^{3} S_{2} \\ 3 & S_{7} S_{2} & 11 & S_{7}^{2} S_{2} S_{7}^{5} S_{2} & 19 & S_{2} S_{7}^{3} S_{2} \\ 4 & S_{7}^{2} S_{2} & 12 & S_{7}^{3} S_{2} S_{7}^{5} S_{2} & 20 & S_{7} S_{2} S_{7}^{3} S_{2} \\ 5 & S_{7}^{3} S_{2} & 13 & S_{7}^{6} S_{2} S_{7}^{4} S_{2} & 21 & S_{2} S_{7}^{2} S_{2} \\ 6 & S_{7}^{4} S_{2} & 14 & S_{2} S_{7}^{4} S_{2} & 22 & S_{7}^{6} S_{2} S_{7}^{2} S_{2} \\ 7 & S_{7}^{5} S_{2} & 15 & S_{7} S_{2} S_{7}^{4} S_{2} & 23 & S_{7}^{5} S_{2} S_{7}^{2} S_{2} \\ 8 & S_{7}^{6} S_{2} & 16 & S_{7}^{2} S_{2} S_{7}^{4} S_{2} & 24 & S_{2} S_{7}^{4} S_{2} S_{7}^{2} S_{2} . \end{matrix}

The representation of the special group is derived from this general ﬁgure by retaining only a set of $168$ white (and corresponding black) triangles, which are distinct when $S_{2}$ , $S_{3}$ and $S_{7}$ are replaced by the corresponding substitutions given on p. 882. When each white triangle is thus marked with the corresponding substitution, it is found that a complete set of $168$ distinct white (and black) triangles is given by the portion of the ﬁgure actually drawn and the six other distinct portions obtained by rotating it round the centre of the orthogonal circle through multiples of $\frac{2}{7} π$ .

To complete the graphical representation of the group of order $168$ , it is necessary to determine the correspondence in pairs of the sides of the boundary. This is facilitated by noticing that the angular points $A_{1}$ , $A_{2}$ , $A_{3}$ , … of the boundary must correspond in sets. Now the white triangle, which has an angle at $A_{1}$ and lies inside the polygon, is given by

S_{2} S_{7}^{4} S_{2} S_{7}^{2} S_{2} .

This must be equivalent to a white triangle, which lies outside the polygon, and has a side on the boundary and an angle at one of the points $A_{2}$ , $A_{3}$ , ….

The triangle, which satisﬁes these conditions and has an angle at $A_{2 n + 1}$ , is given by

S_{7} S_{2} S_{7}^{4} S_{2} S_{7}^{2} S_{2} S_{7}^{n};

while the triangle, which satisﬁes the conditions and has an angle at

A_{2 n + 2}

, is given by

S_{7}^{6} S_{2} S_{7}^{5} S_{2} S_{7}^{3} S_{2} S_{7}^{n} .

When $(16) (34)$ and $(1673524)$ are written for $S_{2}$ and $S_{7}$ , we ﬁnd that

S_{2} S_{7}^{4} S_{2} S_{7}^{2} S_{2} = S_{7} S_{2} S_{7}^{4} S_{2} S_{7}^{2} S_{2} S_{7}^{5} .

The white triangle with an angle at $A_{1}$ inside the polygon is therefore equivalent to the white triangle with an angle at $A_{11}$ , which lies outside the polygon and has a side on the boundary. It follows, from the continuity of the ﬁgure, that the arcs $A_{1} A_{2}$ and $A_{11} A_{10}$ of the boundary correspond. Since the operation $S_{7}$ changes the ﬁgure and the boundary into themselves, it follows that $A_{3} A_{4}$ , $A_{13} A_{12}$ ; $A_{5} A_{6}$ , $A_{1} A_{14}$ ; $A_{7} A_{8}$ , $A_{3} A_{2}$ ; $A_{9} A_{10}$ , $A_{5} A_{4}$ ; $A_{11} A_{12}$ , $A_{7} A_{6}$ ; and $A_{13} A_{14}$ , $A_{9} A_{8}$ ; are pairs of corresponding sides. Hence the above single condition is suﬃcient to ensure that the general group shall reduce to the special group of order $168$ .

By taking account of the relation

{(S_{7} S_{2})}^{3} = 1, or {(S_{2} S_{7})}^{3} = 1,

the form of the condition may be simpliﬁed. Thus it may be written

\begin{array}{l} S_{7}^{4} S_{2} S_{7}^{2} S_{2} & = S_{2} S_{7} S_{2} S_{7} \cdot S_{7}^{3} S_{2} S_{7}^{2} S_{2} S_{7}^{5} \\ = S_{7}^{6} S_{2} S_{7}^{3} S_{2} S_{7}^{2} S_{2} S_{7}^{5}, \end{array}

S_{2} S_{7}^{2} S_{2} = S_{7}^{2} S_{2} S_{7}^{3} S_{2} S_{7}^{2} S_{2} S_{7}^{5} .

Now

\begin{array}{l} S_{2} S_{7} \cdot S_{7} S_{2} & = S_{7}^{6} S_{2} S_{7}^{6} S_{2} \cdot S_{2} S_{7}^{6} S_{2} S_{7}^{6} \\ = S_{7}^{6} S_{2} S_{7}^{5} S_{2} S_{7}^{6} . \end{array}

Hence

S_{7}^{4} S_{2} S_{7}^{5} S_{2} S_{7} = S_{2} S_{7}^{3} S_{2} S_{7}^{2} S_{2},

S_{7}^{4} S_{2} S_{7}^{4} \cdot S_{2} S_{7}^{6} S_{2} = S_{2} S_{7}^{3} S_{2} S_{7}^{2} S_{2},

S_{7}^{4} S_{2} S_{7}^{4} S_{2} S_{7}^{4} = S_{2} S_{7}^{3} S_{2},

or ﬁnally

{(S_{7}^{4} S_{2})}^{4} = 1 .

The simple group of order $168$ is therefore deﬁned abstractly by the relations⁸³

S_{2}^{2} = 1, S_{7}^{7} = 1, {(S_{7} S_{2})}^{3} = 1, {(S_{7}^{4} S_{2})}^{4} = 1 .

Ex. Shew that the symmetric group of degree ﬁve is a group of genus four; and that it is completely deﬁned by the relations

S_{2}^{2} = 1, S_{5}^{5} = 1, {(S_{2} S_{5})}^{4} = 1, {(S_{5}^{- 1} S_{2} S_{5} S_{2})}^{3} = 1 .

211. The regular division of a continuous surface into $2 N$ black and white polygons is only one of many methods that may be conceived for representing a group graphically.

We shall now describe shortly another such mode of representation, due to Cayley⁸⁴, who has called it the method of colour-groups. As given by Cayley, this method is entirely independent of the one we have been hitherto dealing with; but there is an intimate relation between them, and the new method can be most readily presented to the reader by deriving it from the old one.

Let

1, S_{1}, S_{2}, \dots, S_{N - 1}

be the operations of a group

G

of order

N

. We may take the

N - 1

operations other than identity as a set of generating operations. Their continued product

S_{1} S_{2} \dots S_{N - 1}

is some deﬁnite operation of the group. If it is the identical operation, the only modiﬁcation in the ﬁgure, which represents the group by the regular division of a continuous surface, will be that the

N

th corner of the polygon has an angle of two right-angles.

With this set of generating operations, the representation of the group is given by a regular division of a continuous surface into $N$ white and $N$ black polygons $A_{1} A_{2} \dots A_{N}$ , the angle at $A_{r}$ being $\frac{2 π}{m_{r}}$ , $m_{r}$ being the order of $S_{r}$ . Suppose now that in each white polygon we mark a deﬁnite point. From the marked point in the polygon $Σ$ , draw a line to the marked point in the polygon derived from it by a positive rotation round its angle $A_{r}$ . Call this line an $S_{r}$ -line, and denote the direction in which it is drawn by means of an arrow. Carry out this construction for each polygon $Σ$ , and for each of its angles except $A_{N}$ . We thus form a ﬁgure which, disregarding the original surface, consists of $N$ points connected by $N (N - 1)$ directed lines, two distinct lines joining each pair of points. Now if the line drawn from $a$ to $b$ , where $a$ and $b$ are two of the points, is an $S$ -line, then the line drawn from $b$ to $a$ is from the construction an $S^{- 1}$ -line. We may then at once modify our diagram, in the direction of simpliﬁcation, by dropping out one of the two lines between $a$ and $b$ , say the $S^{- 1}$ -line, on the understanding that the remaining line, with the arrow-head reversed, will give the line omitted. If $S$ is an operation of order $2$ , $S$ and $S^{- 1}$ are identical, and two arrow-heads may be drawn on such a line in opposite directions. The modiﬁed ﬁgure will now consist of $N$ points connected by $\frac{1}{2} N (N - 1)$ lines. From the construction it follows at once that, for every value of $r$ , a single $S_{r}$ -line ends at each point of the ﬁgure and a single $S_{r}$ -line begins at each point of the ﬁgure; these two lines being identical when the order of $S_{r}$ is $2$ .

We may pass from one point of the ﬁgure to another along the lines in various ways; but any path between two points of the ﬁgure will be speciﬁed completely by such directions as: follow ﬁrst an $S_{r}$ -line, then an $S_{s}$ -line, then an $S_{t}^{- 1}$ -line, and so on. Such a set of directions is said to deﬁne a route. It is an immediate consequence of the construction that, if starting from some one particular point a given route leads back to the starting point, then it will lead back to the starting point from whatever point we begin. In fact, a route will be speciﬁed symbolically by a symbol

S_{u} \dots S_{t}^{- 1} S_{s} S_{r},

and if

S_{u} \dots S_{t}^{- 1} S_{s} S_{r} Σ = Σ,

then

S_{u} \dots S_{t}^{- 1} S_{s} S_{r} = 1,

and therefore

S_{u} \dots S_{t}^{- 1} S_{s} S_{r} Σ' = Σ',

whatever operation

Σ'

may be.

212. If the diagram of $N$ points connected by $\frac{1}{2} N (N - 1)$ directed lines is to appeal readily to the eye, some method must be adopted of easily distinguishing an $S_{r}$ -line from an $S_{s}$ -line. To eﬀect this purpose, Cayley suggested that all the $S_{r}$ -lines should be of one colour, all the $S_{s}$ -lines of another, and so on. Suppose now that, independently of any previous consideration, we have a diagram of $N$ points connected by $\frac{1}{2} N (N - 1)$ coloured directed lines satisfying the following conditions:—

(i) all the lines of any one colour have either ( $a$ ) a single arrow-head denoting their directions: or ( $b$ ) two opposed arrow-heads, in which case each may be regarded as equivalent to two coincident lines in opposite directions;

(ii) there is a single line of any given colour leading to every point in the diagram, and a single line of the colour leading from every point: if the colour is one with double arrow-heads, the two lines are a pair of coincident lines;

(iii) every route which, starting from some one given point in the diagram, is closed, i.e. leads back again to the given point, is closed whatever the starting point.

Then, under these conditions, the diagram represents in graphical form a deﬁnite group of order $N$ .

It is to be noticed that the ﬁrst two conditions are necessary in order that the phrase “a route” used in the third shall have a deﬁnite meaning. Suppose that $R$ and $R'$ are two routes leading from $a$ to $b$ . Then $R {R'}^{- 1}$ is a closed route and will lead back to the initial point whatever it may be. Hence if $R$ leads from $c$ to $d$ , so also must $R'$ ; and therefore $R$ and $R'$ are equivalent routes in the sense that from any given starting point they lead to the same ﬁnal point. There are then, with identity which displaces no point, just $N$ non-equivalent routes on the diagram, and the product of any two of these is a deﬁnite route of the set. The $N$ routes may be regarded as operations performed on the $N$ points; on account of the last property which has been pointed out, they form a group. Moreover, the diagram gives in explicit form the complete multiplication table of the group, for a mere inspection will immediately determine the one-line route which is equivalent to any given route; i.e. the operation of the group which is the same as the product of any set of operations in any given order.

From a slightly diﬀerent point of view, every route will give a permutation of the $N$ points, regarded as a set of symbols, among themselves; no symbol remaining unchanged unless they all do. To the set of $N$ independent routes, there will correspond a set of $N$ substitutions performed on $N$ symbols; and we can therefore immediately from the diagram represent the group as a transitive substitution group of degree $N$ .

213. It cannot be denied that, even for groups of small order, the diagram we have been describing would not be easily grasped by the eye. It may however still be considerably simpliﬁed since, so far as a graphical deﬁnition of the group is concerned, a large number of the lines are always redundant.

If in the diagram consisting of $N$ points and $\frac{1}{2} N (N - 1)$ coloured lines, which satisﬁes the conditions of § 212, all the lines of one or more colours are omitted, two cases may occur. We may still have a ﬁgure in which it is possible to pass along lines from one point to any other; or the points may break up into sets such that those of any one set are connected by lines, while there are no lines which enable us to pass from one set to another.

Suppose, to begin with, that the ﬁrst is the case. There will then, as before, be $N$ non-equivalent routes in the ﬁgure, which form a group when they are regarded as operations; it is obviously the same group as is given by the general ﬁgure. The sole diﬀerence is that there will not now be a one-line route leading from every point to every other point, and therefore the diagram will no longer give directly the result of the product of any number of operations of the group.

If on the other hand the points break up into sets, the new diagram will no longer represent the same group as the original diagram. Some of the routes of the original diagram will not be possible on the new one, but every route on the new one will be a route on the original diagram. Hence the new diagram will give a sub-group; and since it is still the case that no route, except identity, can leave any point unchanged, the number of points in each of the sets must be the same. The reader may verify that the sub-group thus obtained will be self-conjugate, only if the omitted colours interchange these sets bodily among themselves.

214. The simplest diagram that will represent the group will be that which contains the smallest number of colours and at the same time connects all the points. To each colour corresponds a deﬁnite operation of the group (and its inverse). Hence the smallest number of colours is the smallest number of operations that will generate the group. It may be noticed that this simpliﬁed diagram can be actually constructed from the previously obtained representation of the group by the regular division of a surface, the process being exactly the same as that by which the general diagram was obtained. For if

S_{1}, S_{2}, \dots, S_{n}

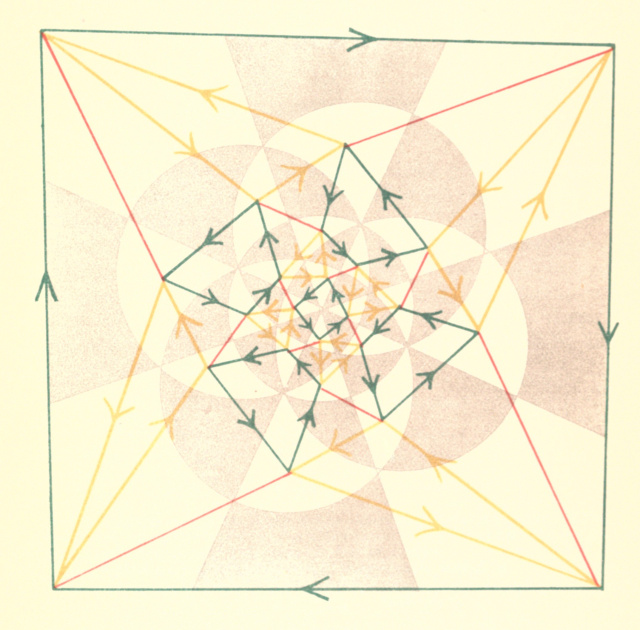
are a set of independent generating operations, and if

S_{1} S_{2} \dots S_{n} S_{n + 1} = 1,

we may represent the group by the regular division of a surface into

2 N

black and white

(n + 1)

-sided polygons. When we draw on this surface the

S_{1}

S_{2}

-, …,

S_{n}

-lines, the

N

points will be connected by lines in a single set, since from

S_{1}, S_{2}, \dots, S_{n}

every operation of the group can be constructed; and the set of points and directed coloured lines so obtained is clearly the diagram required.

As an illustration of this form of graphical representation, we may consider the octohedral group (§ 201), deﬁned by

\begin{matrix} S_{1}^{2} = 1, S_{2}^{3} = 1, S_{3}^{4} = 1, \\ S_{1} S_{2} S_{3} = 1 . \end{matrix}

On the diagram already given (p. 823), we may at once draw $S_{1}$ -, $S_{2}$ - and $S_{3}$ -lines. These in the present ﬁgure are coloured respectively red, yellow, and green. On the lines which correspond to operations of order two (in this case the red lines), the double arrow-heads may be dispensed with. By omitting successively the red, the yellow, and the green lines we form from this the three simplest colour diagrams which will represent the group⁸⁵.

ptail

top

Chapter XIII.On the Graphical Representation of Groups: Groups of Genus Zero and Unity: Cayley’s Colour Groups.

Chapter XIII.
On the Graphical Representation of Groups: Groups of Genus Zero and Unity: Cayley’s Colour Groups.